Mở đầu

Bài viết sẽ đề cập đến các khái niệm và tính chất về phân phối mẫu của tỷ lệ mẫu. Trước khi tiếp tục đọc, các bạn nên nắm rõ về tính chất và công thức của phân phối nhị thức và phân phối chuẩn. Nếu muốn, các bạn có thể đọc bài viết trước về khái niệm này:

Bài viết sẽ sử dụng ngôn ngữ lập trình Python để các bạn có thể tính toán theo, tuy nhiên những bạn không biết lập trình có thể bỏ qua các phần này và tiếp tục đọc .

Phân phối mẫu của tỷ lệ mẫu

Để giải thích khái niệm về mẫu, phân phối mẫu và tính chất trong phân phối mẫu dễ hơn, chúng ta sẽ đưa ra một bài toán ví dụ.

Giả sử chúng ta có một hộp kẹo như ở dưới. Có 10000 viên kẹo trong hộp
1BfQc287jh869Na9KejY0qNGH-sdVe8uZ
Giả sử chúng ta biết trước là tỷ lệ số kẹo màu cam trong hộp là 0.30 (hay 30%).
Để ước lượng tỷ lệ số kẹo màu cam trong hộp, ta lấy 10 viên kẹo trong hộp. 10 viên kẹo này là 1 mẫu kẹo trong hộp:
1KsxQJskeZFt3OHmbMbWMUIDBRFgE2Q5R

Bắt đầu từ biến nhị thức

Với mỗi mẫu 10 viên kẹo, chúng ta sẽ đếm số kẹo có màu cam.
Cần lưu ý là chúng ta biết là tỷ lệ số kẹo màu cam trong hộp là 0.3. Với mỗi một viên kẹo chúng ta lấy ra, ta sẽ có xác xuất viên kẹo đó là màu cam (0.3) hay không (1 - 0.3 = 0.7). Vậy việc lấy một viên kẹo bất kỳ trong hộp có thể được thể hiện bằng một biến xác xuất.

Tiếp đó, việc lấy mẫu 10 viên kẹo và đếm số viên kẹo màu cam trong mẫu đó sẽ cho chúng ta một biến nhị thức. Các điều kiện để biết biến xác xuất nhị thức:

  1. Số lần thí nghiệm là hằng số không thay đổi. Vì chúng ta luôn lấy mẫu là 10 viên kẹo nên số lần thí nghiệm sẽ là 10, một hằng số không đổi
  2. Các thí nghiệm độc lập. Vì chúng ta lấy mẫũ 10 viên kẹo không hoàn lại, 10/10000 là 0.1% nhỏ hơn 10%. Dựa vào luật 10%, nếu số mẫu nhỏ hơn 10% so với số tổ hợp, ta có thể coi là thí nghiệm là độc lập.
  3. Xác xuất thành công không thay đổi cho mỗi thí nghiệm. Dựa vào luật 10% ở trên, mỗi lần lấy một viên kẹo, ta sẽ coi kết quả lần lấy kẹo lần trước **không ảnh hưởng đáng kể ** đến xác xuất lấy được viên kẹo màu cam tiếp theo. Tưởng tượng trường hợp ta 9 viên kẹo lấy trước đều là màu cam, và bây giờ ta lấy viên thứ 10. Đúng ra, xác xuất lấy viên kẹo màu cam lần thứ 10 sẽ nhỏ hơn xác xuất lấy viên kẹo lần đầu. Trong hộp kẹo có 10000 viên thì 3000 viên kẹo là màu cam (tỷ lệ 0.3). Xác xuất lấy viên thứ 10 theo màu cam sẽ là (3000 - 9)/(10000-9) = 0.29936, vẫn gần là 0.3, nên ta coi xác xuất không thay đổi
  4. Sau mỗi thí nghiệm ta biết kết qủa của thí nghiệm là thành công hay thất bại. Vì nếu lấy được viên kẹo màu cam chúng ta sẽ coi là thành công; không lấy được viên kẹo màu cam chúng ta sẽ coi là thất bại.

Với phân phối nhị thức, nhớ đến công thức tính trung bình và độ lệch chuẩn như sau:

Công thức tính trung bình cho phân phối nhị thức:

\( \mu = n * p \)
Công thức tính độ lệch chuẩn cho phân phối nhị thức:
\( \sigma = \sqrt{n * p * (1-p)} \)

  • Trong đó \( p \) là xác xuất, trong bài toán này là là tỷ lệ của tổ hợp. Trong thực tế hay dùng tỷ lệ của mẫu khi không biết tỷ lệ của tổ hợp
  • \( n \) là số lần thí nghiệm, trong bài toán này là số giá trị có trong mẫu

Công thức trên sẽ tính trung bình và độ lệch chuẩn cho tổng số kẹo màu cam trong mười viên kẹo. Tuy nhiên ta muốn tính trung bình và độ lệch chuẩu của tỷ lệ số kẹo màu cam trong mẫu kẹo đó.

Để tính tỷ lệ số viên kẹo màu cam trong mẫu, đơn giản ta chỉ cần lấy tổngsố viên kẹo màu cam chia cho số viên kẹo trong mẫu. Ví dụ, ở mẫu trên số viên kẹo màu cam trong mẫu là 2, số viên kẹo trong mẫu là 10 nên tỷ lệ của viên kẹo màu cam trong mẫu sẽ là là 2/10 = 0.2 = 20%

Tương tự như vậy, để tính trung bình và độ lệch chuẩn của tỷ lệ trong mẫu, chỉ cần chia số thông kê đó cho n (số giá trị của mẫu)
\( \mu = n * p = \frac{n * p}{n} = p \)

\( \sigma = \sqrt{n * p * (1-p)} = \frac{\sqrt{n * p * (1-p)}}{n} = \sqrt{\frac{p * (1-p)}{n}} \)

Áp dụng công thức trên, với mẫu 10 viên kẹo bất kỳ thì trung bình tỷ lệ sẽ là:

\( \mu = p = 0.3 \)

Chú ý p là tỷ lệ của tổ hợp (không phải của mẫu)

Độ lệch chuẩn sẽ gần là:

\( \sigma = = \sqrt{\frac{0.3 * (1-0.3)}{10}} = 0.1449 \)

Phân phối chuẩn

Mỗi lần lấy mẫu, tổng số kẹo màu cam sẽ khác nhau. Do vậy tỷ lệ số kẹo màu cam sẽ khác nhau cho từng mẫu.
Ví dụ mẫu đầu tiên ta có thể thấy 2 viên kẹo màu cam trong 10 viên (tỷ lệ 20%).
Tuy nhiên mẫu thứ hai ta có thể thấy 4 viên kẹo màu cam (40%).
Mẫu thứ ba có thể lấy 10 viên kẹo màu cam (100%) dù xác xuất việc này xảy ra rất thấp
...
Ta có thể lấy 500 mẫu, mội mẫu 10 viên kẹo, và lưu lại tỷ lệ của từng mẫu là một điểm trong biểu đồ tần số. Khi nhìn tổng quát biểu đồ tần số, ta sẽ thấy rằng, phân phối tạo bởi tỷ lệ của các mẫu này là một phân phối chuẩn.

Có thể thử nghiệm việc này bằng code python.

orange_candy_prob = 0.3
sample_size = 10
num_samples = 500
ratio_samples = []
for i in range(num_samples):
    # Biến nhị thức cho ra tổng số kẹo màu cam
    orange_candy_sample_total = np.random.binomial(sample_size, orange_candy_prob)
    # Tính tỷ lệ số kẹo màu cam trong mẫu
    orange_candy_sample_ratio = orange_candy_sample_total / sample_size
    ratio_samples.append(orange_candy_sample_ratio)
    
import matplotlib.pyplot as plt
plt.subplots(1,1,figsize=(10,7))
plt.hist(ratio_samples, bins=15)
plt.show()

Kết quả của code là biểu đồ tần số (histogram) như dưới, cho thấy phân phối mẫu của tỷ lệ số kẹo màu cam. Phân phối sẽ có hình dạng của phân phối chuẩn

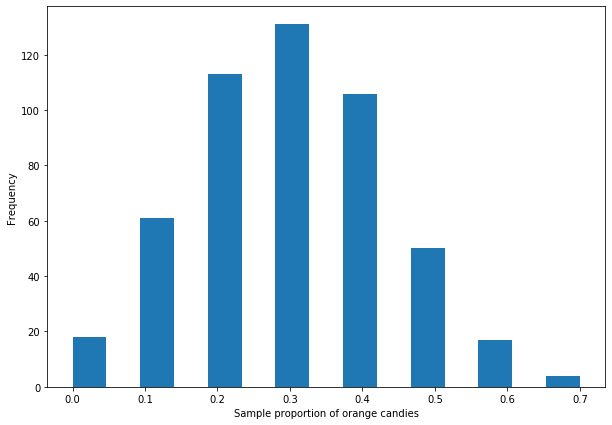
1foBHaZUfHwi_vOU4Jn8swRQkAt4OPfIO

Cụ thể hơn phân phối chuẩn này sẽ có trung bình gần bằng 0.30 và độ lệch chuẩn gần bằng 0.1449 (như tính ở trên sử dụng biến nhị thức)

Có thể kiểm tra bằng code bên dưới:

# Trung bình 
np.asarray(ratio_samples).mean() // 0.2968
# Độ lệch chuẩn
np.asarray(ratio_samples).std() // 0.1443251883768041

Lấy càng nhiều mẫu (10000 thay bằng 500) thì trung bình và độ lệch chuẩn càng giống với số ta tìm được ở công thức trên. Các bạn có thể thử việc này trong code.

Công thức

Tổng hợp lại dưới đây là 2 công thức quan trọng nhất trong bài blog. Các bạn chỉ cần nhớ 2 công thức này là được.

Trung bình cho phân phối mẫu của tỷ lệ mẫu:
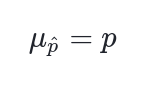
1Yzjn1xplu3EwSsHqLUHO80btMp9R0YWK

Độ lệch chuẩn cho phân phối mẫu của tỷ lệ mẫu:
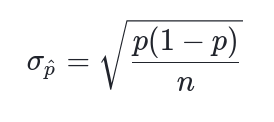
12DAPnz8P8GkzazWSMNAFkhscHXIWPCOX

  • Trong đó p là tỷ lệ của tổ hợp. Trong thực tế, ta có thể dùng tỷ lệ của mẫu khi không biết tỷ lệ của tổ hợp. Nếu có, thì vẫn nên dùng tỷ lệ của tổ hợp.
  • n là số giá trị có trong mẫu

Bài toán

Chúng ta sẽ thử áp dụng những gì vừa học được vào bài toán sau.

Dựa vào một bài khảo sát, 87% người dân Mỹ trên 25 tuổi có bằng cấp 3 (Trung học phổ thông). Giả sử chúng ta lấy một mẫu bất kỳ 200 người Mỹ trong độ tuổi này và tính tỷ lệ người có bằng cấp 3.

Hỏi tỷ lệ người trong mẫu có bằng cấp 3 ít hơn 85% có xác xuất là bao nhiêu?

Đầu tiên, tạo các biến chính từ thông tin trong bài toán:

# Tỷ lệ tổ hợp
p = 0.87
# 
# Số giá trị trong mẫu
n = 200

Tiếp theo tính trung bình và độ lệch chuẩn của phân phối mẫu cho tỷ lệ mẫu dựa vào công thức ở trên.

# Trung bình của phân phối mẫu cho tỷ lệ mẫu
p_sample_dist_mean = p # 0.87
# Độ lệch chuẩn của phân phối mẫu cho tỷ lệ mẫu 
p_sample_dist_stddev = math.sqrt(p*(1-p)/n) # 0.024

Dựa vào trung bình và độ lệch chuẩn, ta có thể vẽ phân phối mẫu như hình sau:
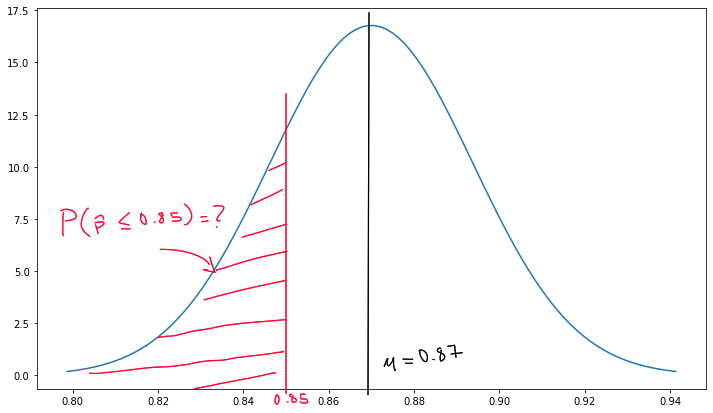
1khiMyvx2pnPuJV5wSvB0YYRCk-HsQHyK

Bài toán yêu cầu tìm xác xuất tỷ lệ người trong mẫu nhỏ hơn 85%. Điều này đồng nghĩa với việc tìm diện tích dưới đường cong trong phân phối chuẩn giữa 0 và 0.85 (diện tích màu đỏ). Dùng lệnh cdf chúng ta sẽ tìm được diện tích này:

prob = stats.norm.cdf(0.85, loc=p_sample_dist_mean, scale=p_sample_dist_stddev)
prob # 0.2001643688581236

Vậy, giả sử bài khảo sát nói đúng, 87% người Mỹ trên 25 tuổi có bằng cấp 3. Nếu chúng ta lấy được một mẫu, có tỷ lệ 85% trở xuống (hoặc dưới 85% * 200 = 170 người) người có bằng cấp 3, xác xuất của việc tìm được mẫu như thế là 20%.

Kết Luận

Hi vọng các bạn đã hiểu được các về các khái niệm và tính chất của phân phối mẫu trong tỷ lệ mẫu. Kiến thức này sẽ giúp các bạn nhiều khi học toán thống kê về sau và công việc liên quan đến phân tích dữ liệu.