Machine Learning - Linear Regression | GMO-Z.com Vietnam Lab Center

Chào mừng tới lớp học, và buổi học đầu tiên của Machine Learning. Hôm nay chúng ta sẽ nhập môn với thuật toán đầu tiên, cũng là người bạn hiền lành nhất trong thế giới Machine Learning — Linear Regression.

Linear Regression

Linear Regression là một thuật toán Supervised Learning, được dùng để dự đoán giá trị liên tục. Nó cố gắng tìm mối quan hệ giữa biến đầu vào $x$ và biến đầu ra $y$ bằng cách vẽ ra một đường thẳng “phù hợp nhất” với dữ liệu.

Phân nhóm các thuật toán Machine Learning - Supervised Learning

Thuật toán này khá đơn giản và chỉ yêu cầu các kiến thức toán học như giải phương trình bậc 1 và đạo hàm cơ bản mà chúng ta đã được học ở ghế nhà trường. Nhưng mà có vẻ tác giả bài viết này không mấy tin tưởng vào trình độ toán học của bạn, nên anh ta quyết định để lại một bài kiểm tra nho nhỏ…

Tìm cực trị của hàm số

Tác giả nghi ngờ trí nhớ đạo hàm của bạn, nên để một câu hỏi nhỏ — hãy nhập giá trị $\textbf{x}$ mà tại đó hàm đạt cực tiểu.

$ \displaystyle f(x) = 2x^2 - 9x + 3 $

$\textbf{x}$ =

Có vẻ như bạn vượt qua bài kiểm tra đầu tiên của tác giả!

Thật ra, đó cũng chính là cốt lõi của Linear Regression. Trong bài toán vừa rồi, bạn tìm giá trị của $x$ sao cho hàm $f(x)$ nhỏ nhất. Linear Regression cũng vậy thôi — chỉ khác là thay vì một ẩn số, giờ ta có nhiều dữ liệu hơn, và thay vì một đường cong đơn giản, ta đang cố tìm một đường thẳng phù hợp nhất với dữ liệu.

Xây dựng bài toán

Giả sử ta có một tập dữ liệu gồm nhiều điểm: $(x_{1}, y_{1}), (x_{2}, y_{2}), (x_{3}, y_{3}), ..., (x_{n}, y_{n})$

Chúng ta cần tìm một đường thẳng $\hat{y}=w_{1}x + w_{0}$ sao cho đường thẳng này gần như đi qua các điểm trong tập dữ liệu đã cho. Cụ thể hơn, chúng ta cần tìm ra 2 số $w_{0},w_{1}$.

Chúng ta đã biết được cách để tìm ra được giá trị đầu vào $x$ của một hàm số $f(x)$ để hàm đạt được giá trị cực tiểu. Vậy thì chúng ta có thể tìm giá trị $w_{0},w_{1}$ để khi một hàm số $f(w_{0},w_{1})$ đạt cực tiểu thì đường thẳng của chúng ta càng gần các điểm trong tập dữ liệu không nhỉ? Đúng hơn, hàm $f(w_{0},w_{1})$ nên là gì để giá trị của hàm càng nhỏ, thì đường thẳng càng khớp với dữ liệu đã cho?

Xét một điểm $(x_{i}, y_{i})$, tại $x=x_{i}$ đường thẳng của chúng ta sẽ đi qua $\hat{y}=w_{1}x_{i} + w_{0}$. Chúng ta cần đường thẳng này đi qua $y_{i}$, vậy nên $(\hat{y}-y_{i})^2$ hay $(w_{1}x_{i} + w_{0}-y_{i})^2$ càng nhỏ thì có nghĩa đường thẳng càng sát với điểm dữ liệu này hơn.

Điều đó có nghĩa là, nếu giá trị của hàm sau càng nhỏ, đường thẳng $\hat{y}=w_{1}x + w_{0}$ sẽ càng gần $n$ điểm trong tập dữ liệu.

$L(w_{0},w_{1})=\sum_{i=1}^{n}(w_{1}x_{i} + w_{0}-y_{i})^2$

Có vẻ như hàm này chưa được tốt lắm, khi tính toán hàm này tôi thấy nhiều bạn đọc bị choáng vì con số quá lớn, vậy nên mình sẽ chia đôi ra nhỉ? Vẫn chưa đủ á? Vậy chắc lấy trung bình là được. Để cho đẹp thì...

$L(w_{0},w_{1})=\frac{1}{2n}\sum_{i=1}^{n}(w_{1}x_{i} + w_{0}-y_{i})^2$

Vậy bây giờ chúng ta chỉ cần tìm cực tiểu của hàm số này là xong!

Thực chất, hàm chúng ta vừa mới định nghĩa ở trên được là hàm mục tiêu hay hàm mất mát (loss function), mỗi một bài toán khác nhau sẽ có hàm mất mát khác nhau, mục đích là tối ưu hóa dựa vào giá trị đầu ra của các hàm này để đạt được mục tiêu của bài toán.
Bây giờ chắc bạn đọc cũng hiểu tại tôi đặt hàm là L thay vì là f nhỉ?

Xem cách tìm cực tiểu của hàm số trên

$\frac{d L}{dw_{1}}=\frac{1}{n}\sum_{i=1}^{n}x_{i}(w_{1}x_{i} + w_{0}-y_{i})=w_{1}\sum_{i=1}^{n}\frac{x_{i}^{2}}{n}+w_{0}\sum_{i=1}^{n}\frac{x_{i}}{n}-\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}$

$\frac{d L}{dw_{0}}=\frac{1}{n}\sum_{i=1}^{n}(w_{1}x_{i} + w_{0}-y_{i})=w_{1}\sum_{i=1}^{n}\frac{x_{i}}{n}+w_{0}-\sum_{i=1}^{n}\frac{y_{i}}{n}$

Đặt $\bar{x}=\sum_{i=1}^{n}\frac{x_{i}}{n}$, $\bar{y}=\sum_{i=1}^{n}\frac{y_{i}}{n}$, $\bar{xy}=\sum_{i=1}^{n}\frac{x_{i}y_{i}}{n}$ và $\bar{x^{2}}=\sum_{i=1}^{n}\frac{x_{i}^{2}}{n}$.

$\frac{d L}{dw_{1}}=w_{1}\bar{x^{2}}+w_{0}\bar{x}-\bar{xy}$

$\frac{d L}{dw_{0}}=w_{1}\bar{x}+w_{0}-\bar{y}$

Tìm điểm dừng $P(w_{0},w_{1})$

$\frac{d L}{dw_{0}}=0 \leftrightarrow w_{0}=\bar{y}-w_{1}\bar{x}$

$\rightarrow\frac{d L}{dw_{1}}=w_{1}\bar{x^{2}}+w_{0}\bar{x}-\bar{xy}=w_{1}\bar{x^{2}}+(\bar{y}-w_{1}\bar{x})\bar{x}-\bar{xy}=w_{1}(\bar{x^{2}}-\bar{x}^2)+\bar{x}\bar{y}-\bar{xy}$

$=w_{1}\bar{x^{2}}+(\bar{y}-w_{1}\bar{x})\bar{x}-\bar{xy}=w_{1}(\bar{x^{2}}-\bar{x}^2)+\bar{x}\bar{y}-\bar{xy}$

$\frac{d L}{dw_{1}}=0 \leftrightarrow w_{1}=\frac{\bar{xy}-\bar{x}\bar{y}}{(\bar{x^{2}}-\bar{x}^2)}$

Vậy chúng ta tìm được nghiệm $w_{1},w_{0}$ như sau:

$w_{1}=\frac{\bar{xy}-\bar{x}\bar{y}}{(\bar{x^{2}}-\bar{x}^2)}$

$w_{0}=\bar{y}-w_{1}\bar{x}$

Với $\bar{x}=\sum_{i=1}^{n}\frac{x_{i}}{n}$, $\bar{y}=\sum_{i=1}^{n}\frac{y_{i}}{n}$, $\bar{xy}=\sum_{i=1}^{n}\frac{x_{i}y_{i}}{n}$ và $\bar{x^{2}}=\sum_{i=1}^{n}\frac{x_{i}^{2}}{n}$.

Chúc mừng, bây giờ bạn đã có thể áp dụng thuật toán Linear Regression này để xây dựng nên một mô hình dự đoán chỉnh chu rồi đấy, các tập dữ liệu trong thế giới thực có mối quan hệ tuyến tính như thế này xuất hiện ở khắp mọi nơi. Thuật toán này cực kỳ hữu ích để tìm ra và mô tả xu hướng ẩn sau những con số tưởng chừng như rời rạc.

Áp dụng thực tế

Hãy tưởng tượng những điểm dữ liệu mà bạn vừa thấy trên màn hình không phải là ngẫu nhiên, mà là các ví dụ thực tế như:

Dự đoán giá nhà: Mỗi điểm là một ngôi nhà, với trục hoành (x) là diện tích (m²) và trục tung (y) là giá bán. Linear Regression sẽ giúp bạn vẽ ra một đường thẳng dự đoán giá của một ngôi nhà bất kỳ dựa trên diện tích của nó.
Dự báo kết quả học tập: Mỗi điểm có thể là một sinh viên, với x là số giờ ôn tập và y là điểm thi. Mô hình sẽ tìm ra đường xu hướng cho thấy việc học nhiều hơn ảnh hưởng đến điểm số như thế nào.
Kinh doanh và Marketing: Các điểm có thể đại diện cho các chiến dịch quảng cáo, với x là chi phí quảng cáo và y là doanh thu mang lại. Mô hình hồi quy tuyến tính sẽ giúp doanh nghiệp ước tính được hiệu quả của việc tăng hay giảm ngân sách quảng cáo.

Trên thực tế, sức mạnh của thuật toán này còn được thể hiện khi mở rộng cho các tập dữ liệu nhiều chiều hơn, cho phép dự đoán một kết quả dựa trên nhiều yếu tố đầu vào cùng lúc.

Thay vì chỉ tìm đường thẳng, chúng ta có thể tìm được một mặt phẳng trong không gian 3D, hay một siêu mặt phẳng trong không gian 4D, 5D, 6D, ... mà khớp với dữ liệu nhất dựa vào thuật toán Linear Regression này.

Tóm lại, Linear Regression là một thuật toán nền tảng nhưng vô cùng mạnh mẽ. Điểm mạnh lớn nhất của nó nằm ở sự đơn giản, dễ diễn giải và tốc độ tính toán nhanh, biến nó thành một công cụ khởi đầu tuyệt vời cho hầu hết các bài toán dự đoán. Tuy nhiên, điều quan trọng cần nhớ là nó hoạt động tốt nhất khi có mối quan hệ tuyến tính rõ ràng trong dữ liệu và có thể nhạy cảm với các giá trị ngoại lai (outliers).

Vậy đây là kết thúc của buổi học Machine Learning đầu tiên rồi. Chúc bạn sẽ nhanh chóng tìm ra được mô hình phù hợp trong không gian 69D của riêng mình nhờ thuật toán này!

...

Khoan, ý bạn là sao khi bạn hết giấy để viết đạo hàm 69 lần. Chúng ta đâu cần phải làm thế, bạn chỉ cần... Khoan, bạn đọc của chúng ta đã biết Đại số tuyến tính chưa?

Đại số tuyến tính - nhân ma trận

Bạn có biết Đại số tuyến tính không?

$$ \begin{pmatrix} 2 & 1 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 5 \\ 6 \end{pmatrix} = ? $$

Nhập kết quả là một ma trận cột

Khái quát hóa thành bài toán nhiều chiều

Chúng ta hãy bắt đầu bằng phương trình mặt phẳng ở không gian 3D, thông thường chúng ta được học phương trình $z=ax+by+c$, thực chất có thể viết lại thành $y=w_{1}x_{1}+w_{2}x_{2}+w_{0}$. Tương tự, chúng ta có phương trình của các siêu mặt phẳng 4D, 5D, ... là:

$y=w_{0}+w_{1}x_{1}+w_{2}x_{2}+\dots+w_{d}x_{d}$

Với $d$ là số chiều

Bây giờ chúng ta đặt $\textbf{x},\textbf{w}$ là 2 vector, $\textbf{x}=\left[\begin{matrix}x_0\\x_1\\x_2\\\dots\\x_d\end{matrix}\right]$ với $x_0=1$ và $\textbf{w}=\left[\begin{matrix}w_0\\w_1\\w_2\\\dots\\w_d\end{matrix}\right]$, nếu bạn biết phép nhân ma trận, thì phương trình ở trên trở thành:

$y=w^{T}x$

Đẹp phải không nào?

Và với tập dữ liệu, đầu vào ($x$) của chúng ta không chỉ là tập hợp các số $[x_0, x_1, x_2, ..., x_n]$ nữa, mà là tập hợp các vector:

$X=\left[\begin{matrix}x_{10}&x_{20}&\dots&x_{n0}\\x_{11}&x_{21}&\dots&x_{n1}\\x_{12}&x_{22}&\dots&x_{n2}\\\vdots&\vdots&\vdots&\vdots\\x_{1d}&x_{2d}&\dots&x_{nd}\end{matrix}\right]=\left[\begin{matrix}1&1&\dots&1\\x_{11}&x_{21}&\dots&x_{n1}\\x_{12}&x_{22}&\dots&x_{n2}\\\vdots&\vdots&\vdots&\vdots\\x_{1d}&x_{2d}&\dots&x_{nd}\end{matrix}\right]$

Hàm mất mát $L$ có thể viết lại thành:

$L(w)=\frac{1}{2n}\sum_{i=1}^{n}(\hat{y}-y_i)^2=\sum_{i=1}^{n}(w^Tx_i-y_i)^2=\frac{1}{2n}\left\|X^Tw-y\right\|_2^2$

$\left\|x\right\|_2$ là chuẩn 2 của vector $x$, hay còn gọi là độ dài của vector. $\left\|x\right\|_2=\sqrt[]{x^Tx}=\sqrt[]{x_1^2+x_2^2+\dots+x_n^2}$

Đạo hàm theo $w$ của hàm mất mát, sau đó tìm cực trị:

$\frac{\partial L}{\partial w}=\frac{1}{n}X(X^Tw-y)=\frac{1}{n}(XX^Tw-Xy)$

$\frac{\partial L}{\partial w}=0 \leftrightarrow XX^Tw=Xy$

$\leftrightarrow w=(XX^T)^{-1}Xy$

Dễ hiểu đúng không? Giờ thì bạn không còn phải vẽ 96 trang giấy chỉ để tính 69 đạo hàm nữa. Hơn thế, thay vì tự tay nhân từng ma trận, ta có thể tận dụng sức mạnh của NumPy — thư viện tính toán số học cực kỳ mạnh mẽ trong Python — để xử lý mọi phép tính chỉ bằng vài dòng lệnh.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Config
d = 2   # Try 1 for 2D line plot, 2 for 3D surface
n = 200

x = np.random.rand(n, d)
real_w = np.random.rand(d, 1)
real_b = np.random.rand(1)

y = x @ real_w + real_b + np.random.normal(0, 0.01, (n, 1))
y = np.squeeze(y)

X = np.hstack([x, np.ones((n, 1))])

pred_params = np.linalg.pinv(X.T @ X) @ X.T @ y
pred_w = pred_params[:-1].reshape(-1, 1)
pred_b = pred_params[-1]

y_hat = X @ pred_params
mse = np.mean((y - y_hat) ** 2)

# Print results
print("MSE:", mse)
print("Real w:", real_w.ravel())
print("Predicted w:", pred_w.ravel())
print("Real b:", real_b.item())
print("Predicted b:", pred_b.item())
print("||w diff||:", np.linalg.norm(real_w - pred_w))
print("|b diff|:", abs(real_b - pred_b))

Ở đây phép tính sẽ bị ngược với công thức phía trên, bởi vì chúng ta đang khởi tạo x và w là một ma trận của các vector hàng, chứ không phải là vector cột.

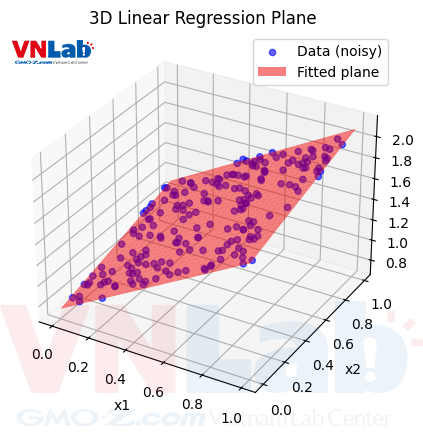
Quá đơn giản phải không nào? Bây giờ chỉ có ai không biết giải phương trình mới không làm được các bài toán dạng Linear Regression. Mà thật ra nếu có không biết, chúng ta vẫn còn một thuật toán được gọi là Gradient Descent để tìm được cực trị, nên không cần phải lo về việc biết giải phương trình đâu. À khoan, bạn có biết Gradient Descent không? - Hãy đợi part 2