Giới thiệu
Bài viết sẽ đề cập về các khái niệm cơ bản liên quan đến toán thống kê:
- Định lý giới hạn trung tâm
- Phân phối mẫu của trung bình mẫu.
- Công thức trung bình và độ lệch chuẩn.
Kiến thức về phân phối chuẩn là cần thiết. Các bạn có thể xem ở bài viết sau:
phân phối và tính chất
Các bạn có thể tham khảo trước bài phân phối mẫu của tỷ lệ mẫu để làm quen dễ hơn với khái niệm đề cập ở đây:
phân phối của tỷ lệ mẫu
Định lý giới hạn trung tâm
Có 3 điểm quan trọng:
- Phân phối mẫu của trung bình mẫu được tạo bằng cách lấy nhiều mẫu . Tính trung bình của từng mẫu với kích thước đủ lớn.
Phân phối mẫu của trung bình mẫulà phân phối chuẩn- Theo định lý giới hạn trung tâm: Trung bình của
phân phối mẫu của trung bình mẫubằng với trung bình của tổ hợp
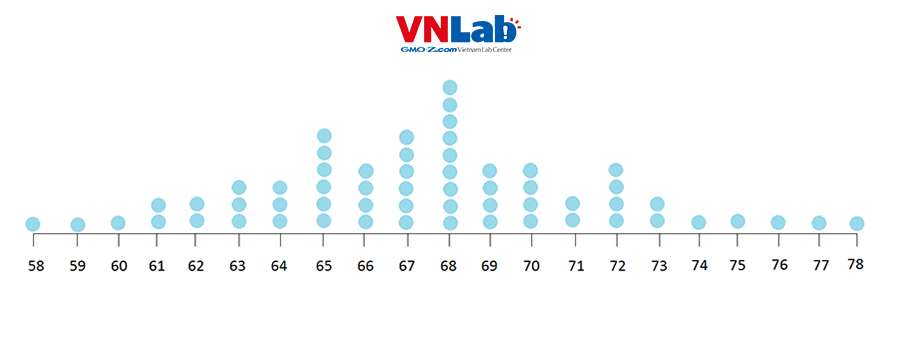
Ban đầu chúng ta có phân phối của tổ hợp, phân phối của tổ hợp không nhất thiết phải là phân phối chuẩn.
Ta lấy mẫu một mẫu từ tổ hợp dữ liệu trên với với kích thước đủ lớn và tính trung bình của mẫu đó, gọi là trung bình mẫu.
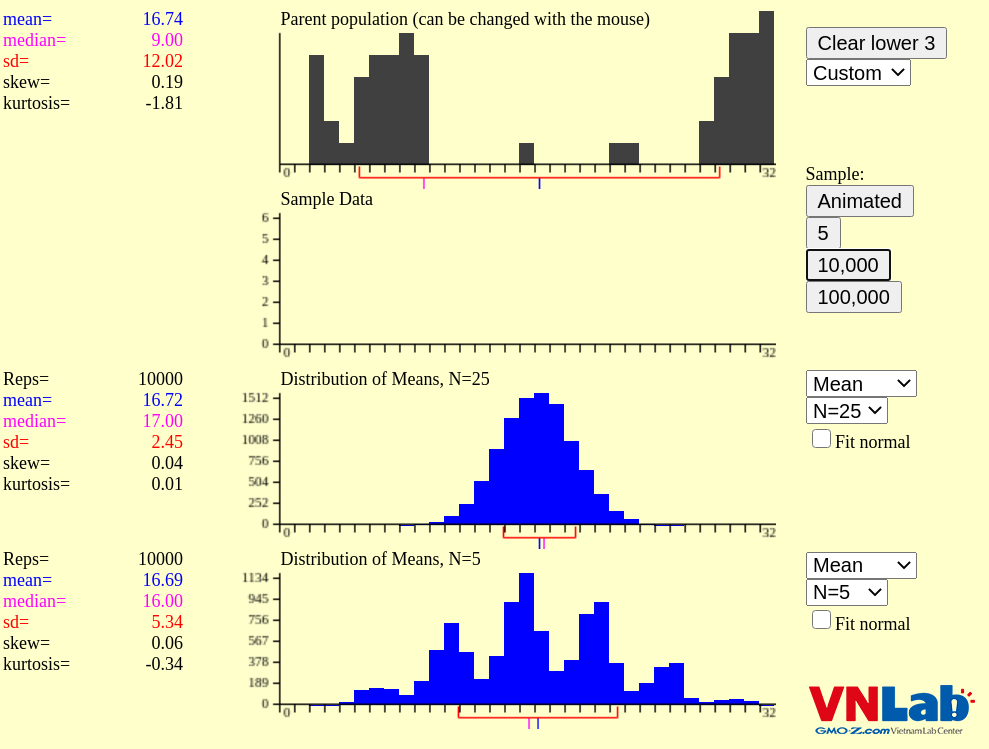
Lấy ví dụ, ta có phân phối của tổ hợp không phải phân phối chuẩn (có 2 đỉnh). Ta lấy một mẫu có kích thước là 25 giá trị, lấy ngẫu nhiên từ tổ hợp. Từ mẫu có kích thước 25, ta có thể tính được một giá trị trung bình mẫu vễ trên biểu đồ tần số (thể hiện bằng ô màu xanh nước biển).
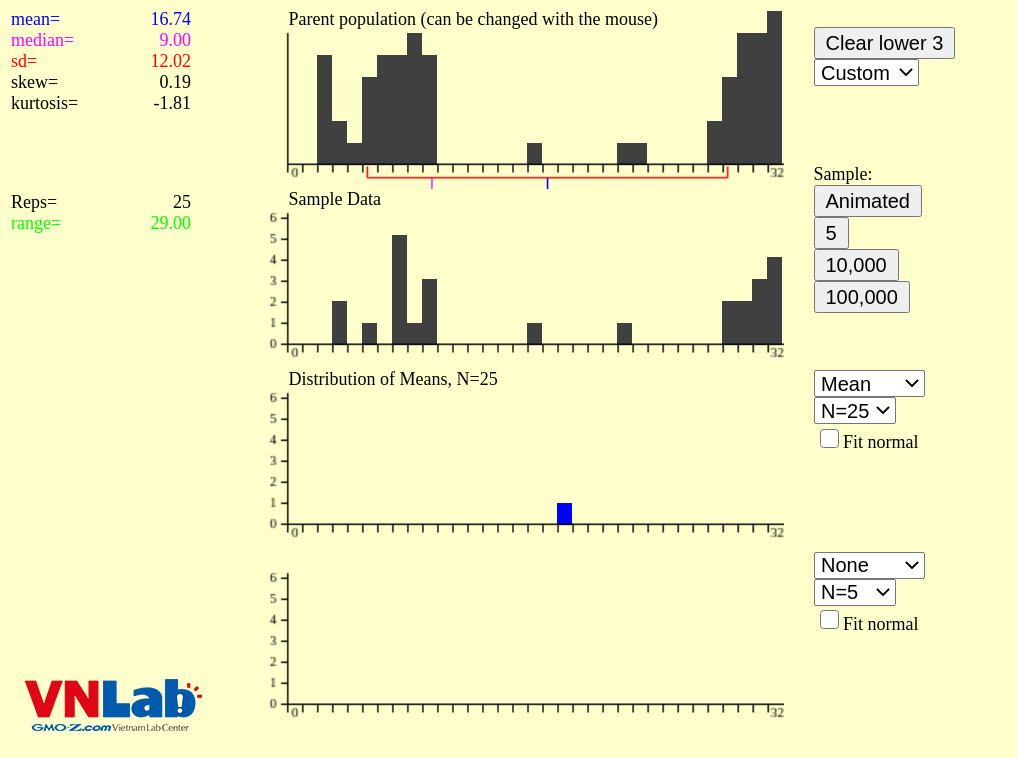
Lặp lại việc lấy mẫu, tính trung bình nhiều lần thì ta sẽ có một phân phối tính được từ các giá trị trung bình. Phân phối này, gọi là phân phối mẫu của trung bình mẫu. Phân phối mẫu của trung bình mẫu sẽ là phân phối chuẩn.
Ví dụ, lấy 6 mẫu kích thước là 25, tính trung bình cho từng mẫu. Sẽ cho ta phân phối trông như dưới. Hiện giờ thì vẫn chưa phải là phân phối chuẩn vì số mẫu lấy quá ít
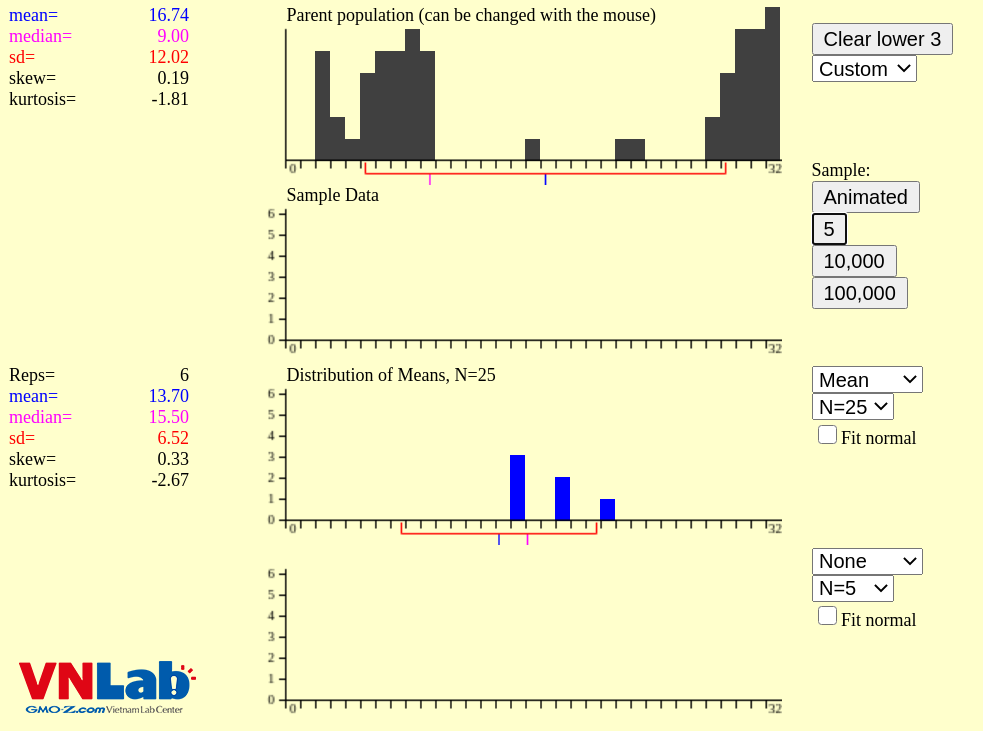
Ví dụ tiếp theo, lấy 10,000 mẫu, mỗi mẫu kích thước 25, tính trung bình. Từ biểu đồ tần suất, ta sẽ thấy phân phối mẫu là phân phối chuẩn.
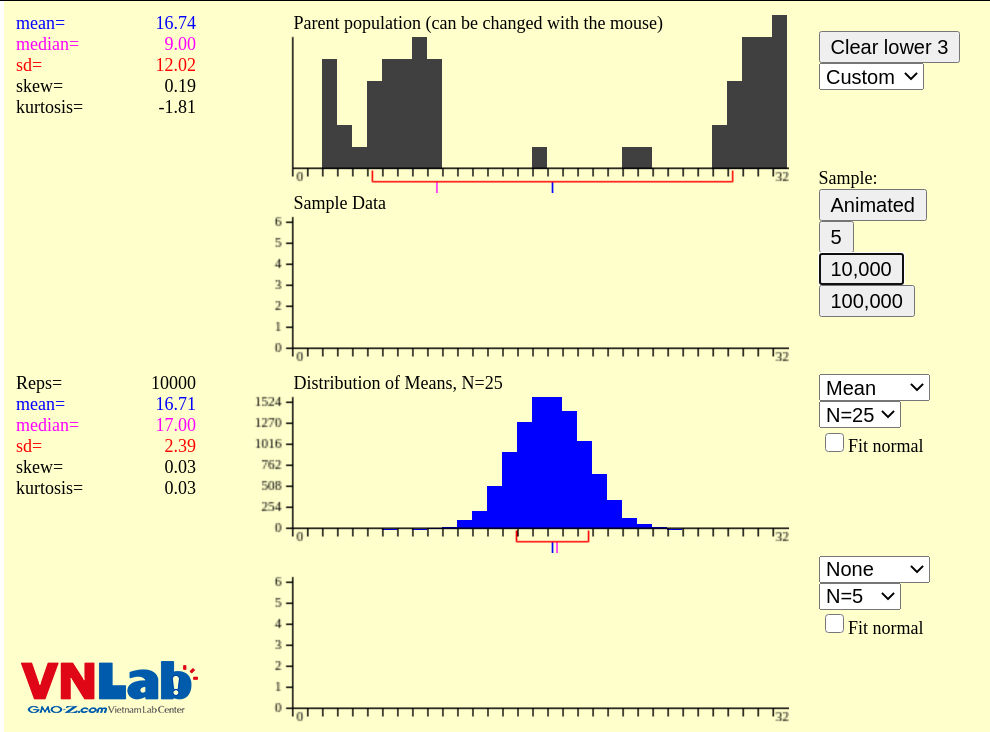
Theo nguyên tắc, nếu lấy kích thước mẫu >=30 ta sẽ có phân phối mẫu của trung bình mẫu là phân phối chuẩn. Một số trường hợp, chỉ cần lấy mẫu >= 20 là ta có thể lấy được phân phối mẫu là phân phối chuẩn.
Nếu lấy mẫu với kích thước nhỏ hơn 20, như kích thước N=5 của hình ở dưới thì ta sẽ ít khả năng có phân phối chuẩn. Như ví dụ sau, phân phối N=5 không phải là phân phối chuẩn, kể cả nếu lấy mẫu 10000 lần.
Công thức
Phân phối mẫu của trung bình mẫu là phân phối chuẩn, nên sẽ có 2 giá trị thống kê quan trọng: trung bình và độ lệch chuẩn
Trung bình của phân phối mẫu
\( \mu = \mu_{\overline{x}} \)
Trong đó:
- \( \overline{x} \) là trung bình mẫu
- \( \mu_{\overline{x}} \) là trung bình của phân phối mẫu của trung bình mẫu
- \( \mu \) là trung bình của tổ hợp
- \( n \) là kích thước mẫu
Độ lệch chuẩn của phân phối mẫu
\( \sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}} = \frac{s}{\sqrt{n}} \)
Trong đó:
- \( \overline{x} \) là trung bình mẫu
- \( \sigma_{\overline{x}} \) là độ lệch chuẩn của phân phối mẫu của trung bình mẫu
- \( \sigma \) là độ lệch chuẩn của tổ hợp
- \( n \) là kích thước mẫu
- \( s \) là độ lệch chuẩn của mẫu. Trên thực tế rất ít khi chúng ta biết độ lệch chuẩn của tổ hợp, nên thường hay dùng độ lệch chuẩn của mẫu
Áp dụng công thức
Quay trở lại phân phối mẫu của trung bình mẫu. Nhớ là ta lấy mẫu với kích thước là 25.
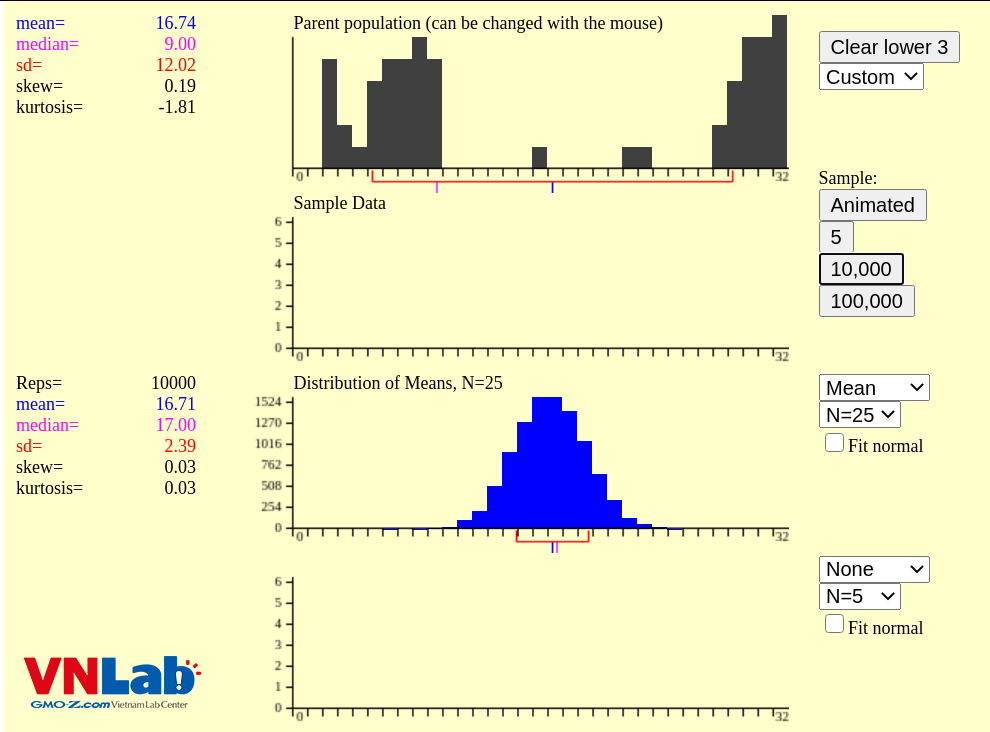
Công thức trung bình của phân phối mẫu:
\( \mu_{\overline{x}} = \mu = 16.74 \)
Công thức tính độ lệch chuẩn của phân phối mẫu:
\( \sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}} = \frac{12.02}{\sqrt{25}} = 2.404 \)
Sử dụng công thức ta sẽ tính được phân phối mẫu của trung bình là phân phối chuẩn, có trung bình là 16.74 và độ lệch chuẩn là gần bằng 2.40. Trong thực nghiệm, trung bình của phân phối mẫu là 16.71, độ lệch chuẩn là 2.39 (mean, sd của phân phối mẫu trong hình N=25). Con số chúng ta tìm được gần bằng con số thực nghiệm.
Thay bằng lẫy mẫu 10,000 lần, nếu lấy mẫu 100,000 lần ta sẽ có con số chính xác, gần với thực tế hơn.
Kết luận
Hi vọng các bạn nắm được khái niệm về cách tính các giá trị của phân phối mẫu của trung bình mẫu. Đây là một trong những khái niệm quan trọng sử dụng nhiều trong toán thống kê và data science
Các bạn có thể đọc thêm các bài viết sau để hiểu về cách áp dụng phân phối mẫu của trung bình mẫu: