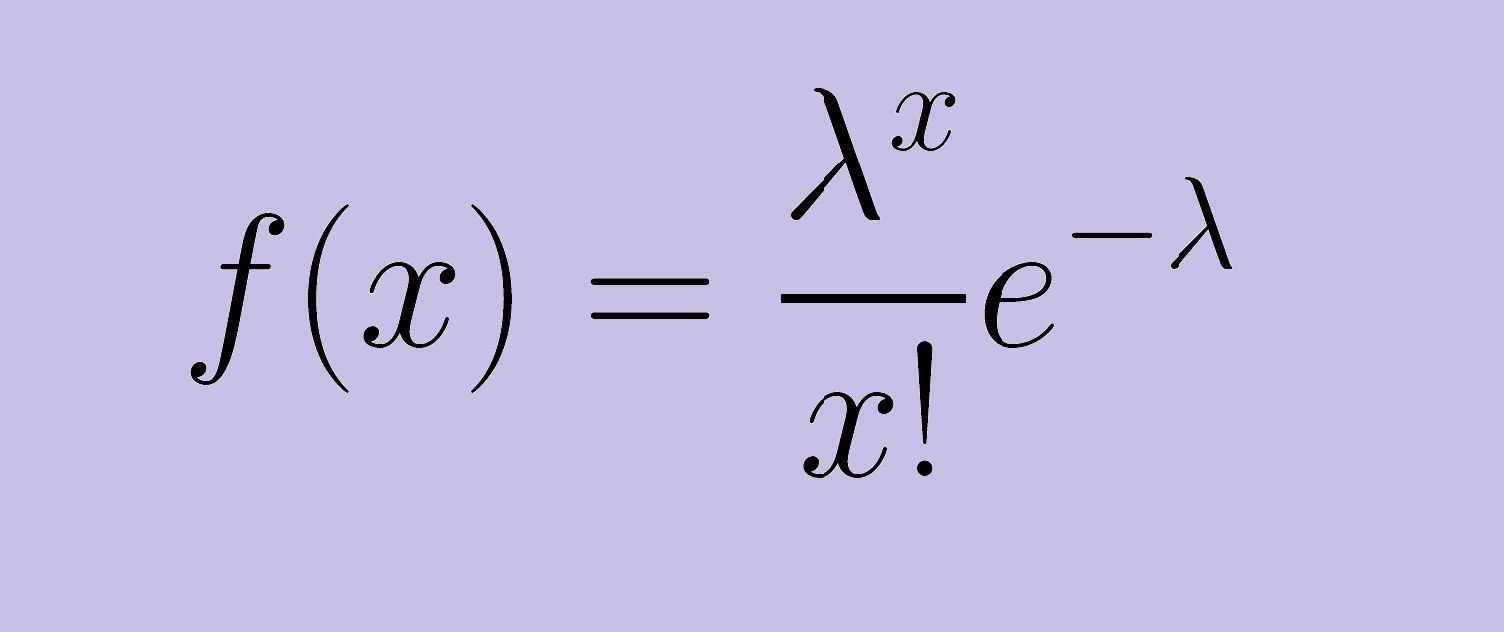Phân phối Poisson là gì?
Nếu lấy định nghĩa về phân phối Poisson từ wiki, sẽ thấy khó hiểu:
Phân phối Poisson (phân phối Poa-dông) là một phân phối xác suất rời rạc. Nó khác với các phân phối xác suất rời rạc khác ở chỗ thông tin cho biết không phải là xác suất để một sự kiện (event) xảy ra (thành công) trong một lần thử như trong phân phối Bernoulli, hay là số lần mà sự kiện đó xảy ra trong n lần thử như trong phân phối nhị thức, mà chính là trung bình số lần xảy ra thành công của một sự kiện trong một khoảng thời gian nhất định. Giá trị trung bình này được gọi là lamda
Theo cách hiểu đơn giản, phân phối Poisson là phân phối cho biết xác xuất của sự kiện rời rạc xảy ra nhiều lần tại thời điểm ngẫu nhiên, trong một khoảng thời gian quy định. Sự kiện rời rạc có nghĩa là các sự kiện không ảnh hưởng trực tiếp đến nhau.
Ví dụ bài toán có thể sử dụng phân phối Poisson?
- Xác xuất số khách hàng gọi đến dịch vụ chăm sóc trong 1 tiếng.
- Xác xuất số người click vào link trang web trong 15 phút tới.
Phân phối Poisson trông như thế nào?
Tùy theo giá trị trung bình sự kiện xảy ra (lambda, sẽ được giải thích sau), hình dạng của phân phối Poisson sẽ thay đổi.
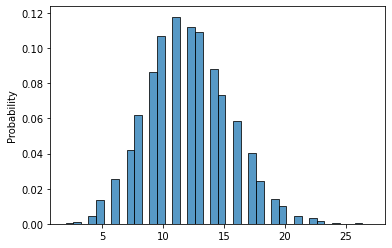
Phân phối Poisson có thể giống phân phối chuẩn. Trục x là số lần sự kiện xảy ra, trục y là xác xuất:
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
s = np.random.poisson(12, 10000)
sns.histplot(s, bins=40, stat="probability")
plt.show()
Hoặc một phần của phân phối chuẩn.
import matplotlib.pyplot as plt
import numpy as np
s = np.random.poisson(2, 10000)
sns.histplot(s, bins=40, stat="probability")
plt.show()
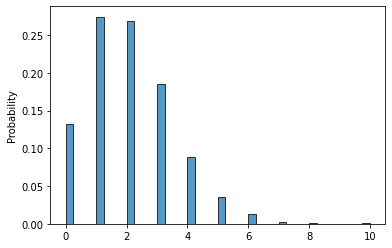
Điểm lưu ý là khác với phân phối chuẩn, phân phối Poisson là phân phối rời rạc. Vì số lần sự kiện xảy ra là số rời rạc (không là 1.2, 2.5, mà phải có số là 1,2,3...).
Tính xác xuất số lần sự kiện xảy ra
Công thức
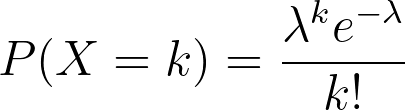
Trong đó:
- \( \lambda \) = giá trị kì vọng xuất hiện của sự kiện trong một khoảng cho sẵn. Thường dựa trên dữ liệu thực tế .
- k = Số lần sự kiện xảy ra (e.g 0,1,2,3...). Số ta muốn tìm hiểu.
- e = số Euler (2.71828...)
Để áp dụng, bài toán cần thỏa mãn điều kiện dưới:
- Các sự kiện xảy ra độc lập: việc sự kiện A xảy ra không ảnh hưởng đến sự kiện B.
- \( \lambda \), giá trị kì vọng sự kiện xảy ra không thay đổi theo thời gian
- Sự kiện có thể xảy ra bất cứ lúc nào.
- Xác xuất sự kiển xảy ra tỷ lệ thuận với khoảng thời gian tính.
Bài toán 1
Tại một cửa hàng tạp hóa, một ngày 8 tiếng làm việc trong giờ hành chính. Nhân viên tại cửa hàng đếm có tổng cộng có 88 khách hàng đến. Hỏi xác xuất một tiếng sau dưới 1 khách hàng đến là bao nhiêu?
Đầu tiên, ta kiểm tra thỏa mãn điều kiện:
- Các sự kiện xảy ra độc lập: khách hàng A đến không ảnh hưởng đến khách hàng B đến hay không.
- Số lần sự kiện không thay đổi theo thời gian: tạm coi rằng giờ hành chính không làm ảnh hưởng đến số lượng khách. Ngược lại, nếu bài toán yêu cầu tính 24 giờ, thì số lượng khách về ban đêm sẽ ít hơn ban ngày, và không thoả mãn điều kiện này.
- Sự kiện có thể xảy ra bất cứ lúc nào: khách hàng có thể đến bất cứ lúc nào trong giờ hành chính. Không theo quy luật.
- Xác xuất sự kiển xảy ra tỷ lệ thuận với khoảng thời gian tính: thời gian tính càng dài, số khách hàng càng nhiều. Ví dụ, số khách hàng đến trong 1 phút là 2, thì 1 tiếng là 2 x 60 = 120.
Tính lambda:
\( \lambda = 88/8 = 11 \)
Chúng ta dùng công thức và giá trị lambda trên, ta tính xác xuất khách hàng đến bằng 0 hoặc bằng 1:
\( P(X \leq 1) = P(X=0) + P(X=1) = 0.0000167 + 0.0001874 +=0.0002004 \)
Tuy nhiên sử dụng code sẽ nhanh hơn và cho kết quả tương tự:
lambda_val = 88/8
prob = poisson.cdf(1, mu=lambda_val)
prob # 0.000200420409482948
Xác xuất dưới một khách đến trong một tiếng sẽ là 0.02%. Bình thường một tiếng có 11 khách, bỗng nhiên có dưới 1 khách đến, về suy luận, thì xác xuất phải rất thấp. Giải bài toán, ta biết chỉ có 0.02% việc này xảy ra ngẫu nhiên. Phải có nguyên nhân khác khiến khách hàng đến ít như vậy (e.g đối thủ cạnh tranh, thời tiết...)
Tính xác xuất thời gian đợi
Công thức
Đôi khi chúng ta không muốn biết xác xuất sự kiện xảy ra với X lần trong một khoảng thời gian là bao nhiêu. Mà chúng ta muốn biết xác xuất thời gian ta phải đợi để sự kiện tiếp theo xảy ra là bao nhiêu
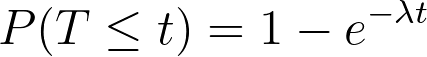
Trong đó:
- \( \lambda \) = giá trị kì vọng xuất hiện của sự kiện trong khoảng thời gian nhất định. Thường dựa trên dữ liệu thực tế
- t = thời gian đến sự kiện xảy ra tiếp theo ta muốn biết.
- e = số Euler (2.71828...)
Bài toán 2
Tại một cửa hàng tạp hóa, một ngày 8 tiếng làm việc trong giờ hành chính. Nhân viên tại cửa hàng đếm có tổng cộng có 88 khách hàng đến. Hỏi: tại thời gian bất kì (trừ cuối giờ hành chính), dưới 15 phút sau xác xuất một khách hàng đến là bao nhiêu?
Bài toán thoả mãn các điều kiện như đã viết ở trên. Chúng ta có thể trực tiếp giải bài toán.
Implement công thức:
import math
"""
Tính xác xuất thời gian đợi đến sự kiện tiếp theo
Parameters:
lambda_val (float): trung bình số sự kiện trên khoảng thời gian (e.g 10 khách hàng/giờ)
time (float): thời gian ta kỳ vọng sự kiện tiếp theo xảy ra. Cùng đơn vị thời gian với lambda_val
is_larger (boolean): True nếu ta tính xác xuất sự kiện tiếp theo xảy ra muộn hơn thời gian kỳ vọng. Xảy ra sớm hơn thì False. Default là False.
Return:
(float): xác xuất sự kiện tiếp theo xảy ra.
```python
def calc_wait_time_prob(lambda_val, time, is_larger=False):
base_calc = math.exp(-lambda_val * time)
if is_larger:
return base_calc
else:
return 1 - base_calc
Giải bài toán
# Tính lambda
lambda_value = 88/6
# Chuyển giá trị về 1 tiếng
time = 15/60
calc_wait_time_prob(lambda_value, time, is_larger=False)
# 0.9744, hoặc 97.4%
Vậy tiếp theo xác xuất khách hàng đến dưới 15 phút là: 97.4%.
Kết bài
Từ bài viết chúng ta đã:
- Hiểu phân phối Poisson là gì, trông như thế nào
- Giải bài toán tính xác xuất số lần sự kiện xảy ra trong một khoảng thời gian
- Giải bài toán tính thời gian tối thiểu cho sự kiện tiếp theo xảy ra.